Added documentation

README.md

@@ -1,2 +1,32 @@
-# rPID
-Partial Information Decomposition for R
+# rPID - Partial Information Decomposition for R
+
+Many biological systems involve multiple interacting factors affecting an outcome synergistically and/or redunantly, e.g. genetic contribution to a phenotype or the tight interplay of genes within a gene-regulatory network (GRN)<sup id="a2">[2](#f2)</sup>. Information theory provides a set of measures that allow us to characterize statistical dependencies between pairs of random variables with considerable advantages over simpler measures such as (Pearson) correlation, as it is capable of capturing non-linear dependencies, and reflecting the dynamics between pairs or groups of genes<sup id="a3">[3](#f3)</sup>. In these settings, we are concerned with the statistics of how two (or more) random variables X<sub>1</sub>, X<sub>2</sub>, called source variables, jointly or separately specify/predict another random variable Z, called a target random variable. The source variables can provide information about the target uniquely, redundantly, or synergistically (see PI-diagram below). The mutual information (I) between the source variables and the target variable is equal to the sum of four partial information terms:
+
+$I(Z; X1; X2) = Synergy(Z; X1, X2) + Unique(Z; X1) + Unique(Z; X2) + Redundancy(Z; X1, X2)$
+
+![Mutual information decomposition](https://github.molgen.mpg.de/raw/loosolab/rPID/master/PI-diagram.png)
+
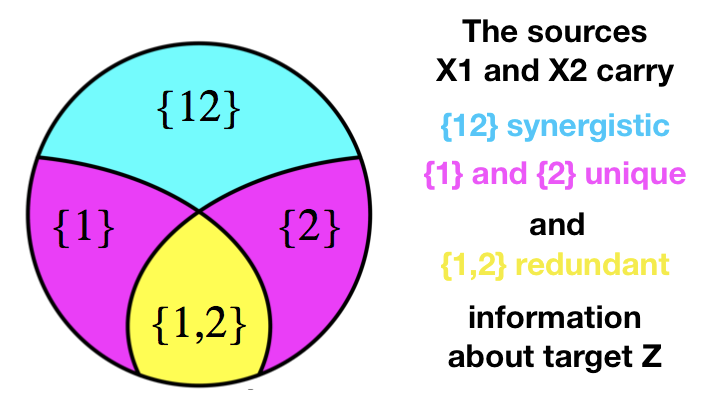+Here, we implemented the nonnegative decomposition of Multivariate Information for three random vectors as proposed by Williams and Beer<sup id="a1">[1](#f1)</sup> as an R package.
+
+## Usage
+
+Given three random vectors `r x1`, `r x2` and `r z`, the PID can be calculated from the `r PID` function.
+
+```r
+library(rPID)
+
+pid <- PID(z, x1, x2)
+```
+
+## Installation
+
+```r
+library(devtools)
+install_github("loosolab/rPID", host="github.molgen.mpg.de")
+```
+
+## Literature
+
+<b id="f1">1</b>Williams PL and Beer RD. Nonnegative Decomposition of Multivariate Information. **arXiv** (2010), https://arxiv.org/abs/1004.2515v1 [↩](#a1)
+<b id="f2">2</b>Griffith V and Ho T. Quantifying Redundant Information in Predicting a Target Random Variable. **Entropy** (2015), doi:10.3390/e17074644 [↩](#a2)
+<b id="f3">3</b>Chan et. al. Network inference and hypotheses-generation from single-cell transcriptomic data using multivariate information measures. **bioRxiv** (2016), doi:10.1101/082099 [↩](#a3)