Resistance of a bar

Resistance of a bar

Regarding the electrons (charge $-e$, effective mass $m$) as a viscous fluid with dynamic viscosity $\eta$ and mass density $\rho$, we solve the Navier-Stokes equations

\[\eta\Delta v+\rho\frac em\nabla\phi=0\]

for the velocity field $v$ in the high-viscosity limit (laminar flow, stationary solution), like the Hagen-Poiseuille flow.

For a bar with width $w$, height $h$, and length $\ell$ the electrostatic potential $\phi$ describes a constant electric field generated by applying a voltage $V$ along the $z$ direction,

\[\phi=-V\frac z\ell.\]

We assume that the boundaries of the bar are perfectly rough such that the component of the drift velocity $v$ parallel to the boundary vanishes. Introducing a parameter

\[\gamma:=-\frac{e/m}{\eta/\rho}\frac{\partial}{\partial z}\phi =\frac{e/m}{\eta/\rho}\frac V\ell\]

and denoting with $v$ the $z$ component of the drift velocity from now on the Navier-Stokes equations boil down to solving Poisson’s equation

\[\Delta v=\gamma,\quad(x,y)\in\Omega\]

subject to the Dirichlet boundary condition

\[v=0,\quad(x,y)\in\partial\Omega\]

where $\Omega$ denotes the rectangular region $0\le x\le w\land0\le y\le h$ for arbitrary but constant $z$.

General solution by series expansion

This problem has a formal solution expressing $\gamma$ by a Fourier series expansion in terms of the eigensystem \(\{\phi_{mn},\lambda_{mn}\}\) of the Laplacian with

\[(\Delta-\lambda_{mn})\phi_{mn}=0.\]

We can write

\[\begin{align*} \gamma &= \sum_{m=1}^\infty\sum_{n=1}^\infty\gamma_{mn}\phi_{mn}, \\ \gamma_{mn} &= \frac{\int_\Omega\gamma\phi_{mn}^*{\rm d}A} {\int_\Omega\left\vert\phi_{mn}\right\vert^2{\rm d}A}, \end{align*}\]

which is in principle valid for arbitrary (suitably well behaved) functions $\gamma=\gamma(x,y)$, not just the constant used here. We express the drift velocity $v(x,y)$ in terms of the eigenfunctions as well,

\[v=\sum_{m=1}^\infty\sum_{n=1}^\infty v_{mn}\phi_{mn}\]

and insert this into our main equation $\Delta v=\gamma$ from above to get

\[\sum_{m=1}^\infty\sum_{n=1}^\infty\lambda_{mn}v_{mn}\phi_{mn} = \sum_{m=1}^\infty\sum_{n=1}^\infty\gamma_{mn}\phi_{mn}.\]

Termwise comparison tells us that \(v_{mn}=\gamma_{mn}/\lambda_{mn}\), and we have the desired answer,

\[v=\sum_{m=1}^\infty\sum_{n=1}^\infty\frac{\gamma_{mn}}{\lambda_{mn}}\phi_{mn}.\]

Eigensystem of the Laplacian

The eigensystem of the Laplacian with the boundary conditions given above is obviously given by

\[\begin{align*} \phi_{mn}&=\sin\left(\pi mx/w\right)\sin\left(\pi ny/h\right),\\ \lambda_{mn}&=\pi^2\left((m/w)^2+(n/h)^2\right), \end{align*}\]

and we get

\[\begin{align*} \int_\Omega\left\vert\phi_{mn}\right\vert^2{\rm d}A &= \int_0^w{\rm d}x\sin^2\left(\pi mx/w\right) \int_0^h{\rm d}y\sin^2\left(\pi ny/h\right) \\ &= \frac{wh}4, \\ \int_\Omega\gamma\phi_{mn}^*{\rm d}A &= \gamma \int_0^w{\rm d}x\sin\left(\pi mx/w\right) \int_0^h{\rm d}y\sin\left(\pi ny/h\right) \\ &= \gamma\frac{wh}{\pi^2} \int_0^\pi{\rm d}x\sin\left(mx\right) \int_0^\pi{\rm d}y\sin\left(ny\right) \\ &= \gamma\frac{wh}{\pi^2}\, \frac{(-1)^{m+1}+1}m\,\frac{(-1)^{n+1}+1}n \\ \Rightarrow\gamma_{mn} &= \frac{4\gamma}{\pi^2} \frac{\left(1-(-1)^m\right)\left(1-(-1)^n\right)}{mn}. \end{align*}\]

We finally obtain

\[v=\frac{4\gamma}{\pi^4}\sum_{m=1}^\infty\sum_{n=1}^\infty \frac{\left(1-(-1)^m\right)\left(1-(-1)^n\right)} {mn\left((m/w)^2+(n/h)^2\right)} \sin\left(\pi mx/w\right)\sin\left(\pi ny/h\right).\]

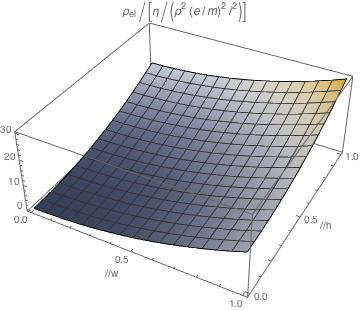
Here is a plot:

Total current and resistance

The total current flowing through the surface $\Omega$ is

\[\begin{align*} I &= \rho\frac e m\int_\Omega v{\rm d}A \\ &= \rho\frac e m \sum_{m=1}^\infty\sum_{n=1}^\infty v_{mn} \int_0^w{\rm d}x\sin(\pi mx/w) \int_0^h{\rm d}y\sin(\pi ny/h) \\ &= \rho\frac e m\frac{wh}{\pi^2} \sum_{m=1}^\infty\sum_{n=1}^\infty v_{mn} \int_0^\pi{\rm d}x\sin\left(mx\right) \int_0^\pi{\rm d}y\sin\left(ny\right) \\ &= \rho\frac e m\frac{wh}{\pi^2} \sum_{m=1}^\infty\sum_{n=1}^\infty v_{mn} \left(\frac{1-(-1)^m}m\right)\left(\frac{1-(-1)^n}n\right) \\ &= V\frac{\rho^2(e/m)^2}\eta\frac{wh}\ell\frac4{\pi^6} \sum_{m=1}^\infty\sum_{n=1}^\infty \frac{\left(1-(-1)^m\right)^2\left(1-(-1)^n\right)^2} {(mn)^2\left((m/w)^2+(n/h)^2\right)}. \end{align*}\]

Terms in the expansion with either $m$ or $n$ even vanish. The first nonvanishing term for $m=n=1$ is already a good approximation to the double sum, so we can approximate

\[I\approx V\frac{64}{\pi^6}\frac{\rho^2(e/m)^2}\eta\frac{wh}\ell \left(\frac1{w^2}+\frac1{h^2}\right)^{-1}.\]

The resistance $R=V/I$ is thus given by

\[\fbox{$\displaystyle R \approx \frac{\pi^6}{64}\frac\eta{\rho^2(e/m)^2} \frac\ell{wh}\left(\frac1{w^2}+\frac1{h^2}\right) $}.\]

See below for a plot of the scaling of the resistivity $\rho_\text{el}:=(wh/\ell)R$ with inverse width $1/w$ and height $1/h$ of the bar (length unit $\ell$).