Saturation fields

The saturation field $H_\text{sat}$, defined as an instability of the fully polarized state towards $\Delta s=1$ spin flips, coming from high fields, can be calculated within a classical approximation, because the fully polarized state, while being an eigenstate to the Hamiltonian, is also the classical state with minimum energy for field $H\ge H_\text{sat}$. We thus regard the pseudospins as classical vectors living on a three-sublattice structure. On each sublattice $i$, any two spins are aligned parallel relative to each other. The direction of each spin defines the $z’$ axis of a local coordinate system, characterized by polar and azimuthal angels $\theta_i$ and $\phi_i$.

The singularities of the Hessian matrix $m_\text H(e)$, $e$ being the classical ground-state energy density per spin,

\[m_\text H(e) :=\frac{\partial^2e}{\partial\{\theta_i,\phi_i\} \partial\{\theta_j,\phi_j\}}\]

include the saturation field as one of the solutions to

\[\det m_\text H(e)=0.\]

In general, the above expression contains up to six zeros, however we will see that things simplify considerably here. Note on the illustrations below: The three thin black arrows in each figure refer to the three sublattice moments where on each sublattice the individual moments are arranged pariwise parallel (ferromagnetically). The thick black arrow denotes the direction of the applied magnetic field $\mu_0H$. The gray rectangles in the last two illustrations denote the coplanar arrangement of all moments.

Field parallel to the trigonal axis

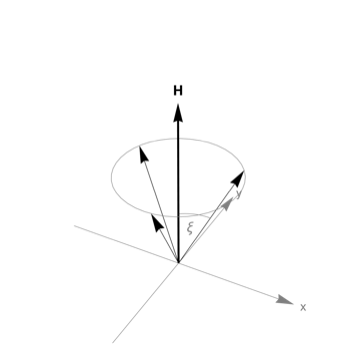
By symmetry (see also the figure above), for the classical ground state, polar angles are all $\theta_i=\xi$, azimuthal angles are $\alpha$ and $\alpha\pm2\pi/3$ such that $|\phi_i-\phi_j|=2\pi/3$. With $h_\parallel:=g_\parallel\mu_\text B\mu_0H$ the ground-state energy density per spin for this case is given by

\[e_\parallel=3sJ_\perp\sin^2\xi \underbrace{\cos\left(\frac{2\pi}3\right)}_{-1/2} +3sJ_\parallel\cos^2\xi-h_\parallel\cos\xi.\]

The nonzero «block» of the Hessian matrix $m_\text H$ reduces to a scalar, $m_\text H(e_\parallel)=\partial^2e_\parallel/\partial\xi^2$, and with $h_\alpha:=g_\alpha\mu_\text B\mu_0H_\alpha$ the determinant above reduces to $(3/2)sJ_\perp+3sJ_\parallel-(1/2)h_\parallel=0$ which gives

\[\mu_0H_\text{sat}^\parallel = \frac{3s^2}{M_\text{sat}^\parallel}\left(J_\perp+2J_\parallel\right)\]

introducing the saturation moment $M_\text{sat}^\parallel=g_\parallel\mu_\text Bs$.

Near saturation, all moments deviate only slightly from the field direction, and $\xi\ll1$. In this case we can also write

\[e_\parallel \approx 3sJ_\parallel-h_\parallel -\xi^2\left(\frac32sJ_\perp+3sJ_\parallel -\frac12h_\parallel\right).\]

This has a quite intuitive form: The first two terms are the ground-state energy at or above saturation: energy loss $3sJ_\parallel$ due to ferromagnetic alignment of the sublattice moments, energy gain $h_\parallel$ due to the alignment parallel to the applied field. Slightly below saturation ($\xi>0$) we gain an energy $(3/2)sJ_\perp\xi^2$ due to components of the sublattice moments in the plane perpendicular to the field direction. This is half of the maximum energy we would obtain if it were possible to align all three sublattice moments in an antiparallel way. We also gain energy $3sJ_\parallel\xi^2$ because of the reduction of the ferromagnetic alignment of the three sublattice moments. At the same time we lose energy $(1/2)h_\parallel\xi^2$.

Field perpendicular to the trigonal axis

This case is a bit more involved as it includes breaking of the $\text C_3$ rotational symmetry of the lattice. We don’t know a priori whether the moments form a distorted-umbrella shape or a planar structure when reducing the field slightly below saturation. We introduce angles $\delta_i:=\pi/2-\theta_i$ and $\epsilon_i:=\alpha-\phi_i$. Then we can write

\[\begin{split} e_\perp &= e_{12}+e_{23}+e_{31}, \\ e_{ij} &:= sJ_\perp\cos\delta_i\cos\delta_j \cos\left(\epsilon_i-\epsilon_j\right) +sJ_\parallel\sin\delta_i\sin\delta_j \\ &\phantom{:=} -\frac16h_\perp\left( \cos\delta_i\cos\epsilon_i +\cos\delta_j\cos\epsilon_j\right) \\ &= e_{ji}. \end{split}\]

In the limit $\delta_i,\epsilon_i\to0$ (full polarization), the determinant of the Hessian reads

\[\left(h_\perp-9sJ_\perp\right)^2 \left[h_\perp-3s\left(J_\parallel+2J_\perp\right)\right]^2 \left[h_\perp-6s\left(J_\perp-J_\parallel\right)\right] h_\perp =0.\]

So we have four singularities. Obviously $h_\perp=0$ is unphysical. Also the solution $h_\perp=6s\left(J_\perp-J_\parallel\right)$ doesn’t make sense as it implies an energy loss $\propto2sJ_\parallel$ when deviating from full polarization. The solution $h_\perp=9sJ_\perp$ corresponds to a planar structure where all three sublattice moments lie in the plane perpendicular to the trigonal axis (see below). This would be the case for $J_\perp>J_\parallel$. The last option $h_\perp=3s\left(J_\parallel+2J_\perp\right)$ corresponds to a planar structure, too, however this time the sublattice moments lie in a plane which contains the trigonal axis. Here $J_\perp<J_\parallel$.

Geometric interpretation

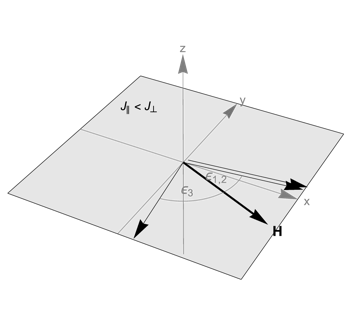
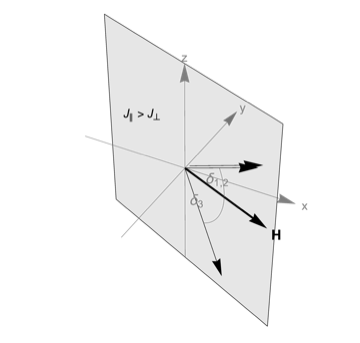
A geometric interpretation can be obtained by looking at two possible planar configurations near $H_\text{sat}$ either in the plane perpendicular to the trigonal axis setting $\delta_i=0$ or in the plane containing the trigonal and the field axis with $\epsilon_i=0$. For the former, the gradient near $H_\text{sat}$ is given by

\[\left(\frac{\partial e_\perp}{\partial\epsilon_i}\right)_{\delta_i=0} \approx \left(\frac{h_\perp}3-2sJ_\perp\right) \begin{pmatrix} \epsilon_1-u\left(\epsilon_2+\epsilon_3\right) \\ \epsilon_2-u\left(\epsilon_3+\epsilon_1\right) \\ \epsilon_3-u\left(\epsilon_1+\epsilon_2\right) \end{pmatrix}\]

with $u:=sJ_\perp/\left[2sJ_\perp-(1/3)h_\perp\right]$. Minimizing this gives

\[\epsilon_1 = \epsilon_2 = \frac u{1-u}\epsilon_3, \quad u = -1\mbox{ or }\frac12.\]

So two sublattice moments are aligned parallel to each other. From $u=-1$ we obtain $h_\perp=9sJ_\perp$ (first factor in the equation above), for $u=1/2$ we obtain the unphysical solution $h_\perp=0$. The ground-state energy density is $e_\perp=3sJ_\perp-h_\perp$. Similar to the case $H\parallel\text c$, we lose energy $3sJ_\perp$ due to the ferromagnetic alignment of all spins, and we gain energy $h_\perp$. Deviating slightly from full polarization, but still with all sublattice moments in the trigonal plane we gain energy $\Delta e_\perp\propto3sJ_\perp|\epsilon_i|$ due to both the small antiferromagnetic component in the spin alignment and the reduction of the moment parallel to the magnetic field.

The gradient near $H_\text{sat}$ for a spin configuration in the plane containing the trigonal axis is given by

\[\left(\frac{\partial e_\perp}{\partial\delta_i}\right)_{\epsilon_i=0} \approx \left(\frac{h_\perp}3-2sJ_\perp\right) \begin{pmatrix} \delta_1-u\left(\delta_2+\delta_3\right) \\ \delta_2-u\left(\delta_3+\delta_1\right) \\ \delta_3-u\left(\delta_1+\delta_2\right) \end{pmatrix}\]

with $u:=sJ_\parallel/\left[2sJ_\perp-(1/3)h_\perp\right]$. Minimizing this gives

\[\delta_1 = \delta_2 = \frac u{1-u}\delta_3, \quad u = -1\mbox{ or }\frac12.\]

From $u=-1$ we obtain $h_\perp=3s\left(J_\parallel+2J_\perp\right)$ (second factor in the equation above). Deviating from full polarization now results in an energy gain $\Delta e_\perp\propto s(J_\parallel+2J_\perp)|\delta_i|$, which is, for $J_\parallel<J_\perp$, smaller than the energy gain when opening the fan in the trigonal plane. For $u=1/2$ we obtain $h_\perp=6s\left(J_\perp-J_\parallel\right)$. This solution is unphysical because this would include an energy loss $\propto2sJ_\parallel$ when deviating from full polarization.

Just for completeness: The isotropic case $J_\perp=J_\parallel$ always corresponds to an umbrella structure, independent of the field direction.