Putting magnetic moments onto a triangular lattice is perhaps the most simple way to create a frustrated system, that is a system "that does not know what to do", given its highly (quasi-) degenerate low-energy excitation spectrum. We calculate thermal properties of the anisotropic triangular lattice based on exact diagonalization of small clusters and compare them with recent experiments.
The most simple model for geometric frustration
The triangular S = 1/2 Heisenberg magnet is the archetypical geometrically
frustrated magnet. It has been studied in countless investigations,
however by now (see the date at the bottom of this page to interpret “now”)
there exists not a single experimental realization of it. Thus allow for
in-plane symmetry breaking and, as always, a small inter-plane coupling,
and quite a few experimentally known compounds can be discussed in the
framework of this model. So let’s introduce an exchange coupling
J2 along one set of parallel triangle sides different from
J1 along the other two triangular directions.
But wait — didn’t we have that J1 J2
business already on the square lattice? Let’s regard the anisotropic
triangular lattice as one of the D2 symmetric siblings of the (D4
symmetric) square lattice model, and reuse what we can from the tools
developed for the latter: All we have to do is to remove every other
J2 bond from the square lattice. If we then introduce an
anisotropy angle like
\[\begin{eqnarray}
J_{1}=J_{\text c}\cos\phi,
&\quad&
J_{2}=J_{\text c}\sin\phi,
\\
J_{\text c}=\sqrt{J_{1}^{2}+J_{2}^{2}},
&\quad&
\phi=\tan^{-1}\left(\frac{J_{2}}{J_{1}}\right)
\nonumber
\end{eqnarray}\]
we can, as a function of φ, interpolate between the standard
Heisenberg magnet (J2 = 0), the isotropic triangle
(J2 = J1), and the one-dimensional chain
(J1 = 0).
Phase diagram
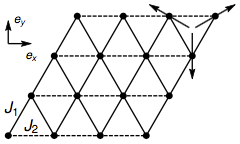
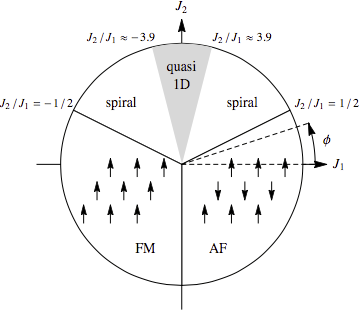
Anisotropic triangular lattice with exchange constants J1 and
J2 and the corresponding phase diagram. The gray sector denotes
the disordered phase around the one-dimensional point, the former is
surrounded by an ordered phase with an incommensurate ordering vector
("spiral"). For small enough values of J2 < *|J1|/2,
the system oders in a commensurate fashion, very similar to the
square-lattice model.*
The characteristic features of the thermodynamic quantities we calculate,
in particular the magnetic susceptibility χ(T) and the specific heat
cV(T), can be used to determine the exchange constants
J1 and J2 of experimental compounds. One example
is given at the top of this page, demonstrating the usefulness of the
finite-temperature Lanczos method which we have used to calculate
χ(T).
Specific heat
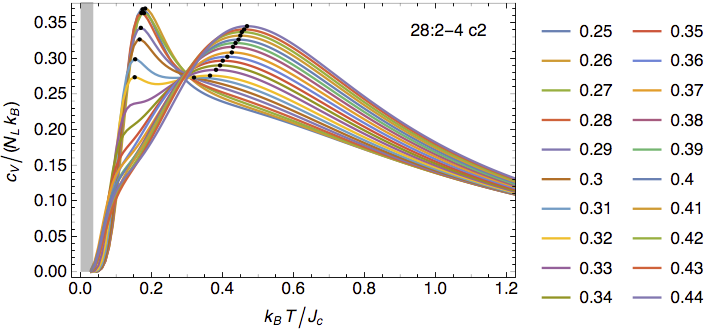
Calculated temperature dependence of the specific heat of the anisotropic
triangular lattice. The curves shown are for values of φ/π between
0.25 (isotropic case, 120-degree ordering) and 0.44 (disordered
quasi-one-dimensional chains). As a function of φ, the characteristic
maximum for the 2D behavior around kBT/Jc = 0.18
gradually vanishes and a second maximum around kBT/Jc
= 0.45 ... 0.5 appears which is characteristic for the one-dimensional
chain where this maximum is exactly at kBT = 0.481 Jc
with cV = 0.35 R. The gray rectangle in the figure denotes the
area where we expect finite-size effects to dominate.
Magnetic susceptibility
In the same way as for the heat capacity, we can calculate the magnetic
susceptibility χ as a function of temperature T and anisotropy
angle φ. Also here we observe a characteristic maximum whose size
and position depend on φ.
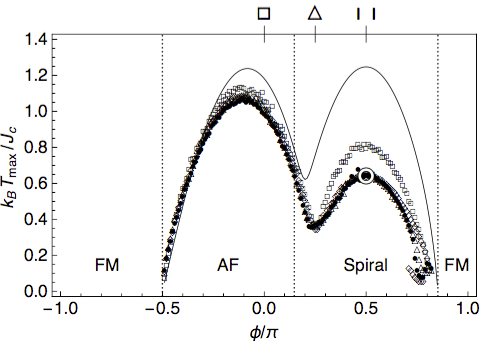
Position T of the characteristic maximum of χ(T) as function of
the anisotropy angle χ, calculated with different tiles between 16
sites (squares) and 28 sites (filled dots). The solid line denotes the
esxact result for a tile with eight sites, the white ring indicates the
Bonner-Fisher result for the one-dimensional chain for comparison.
Comparison with experiments
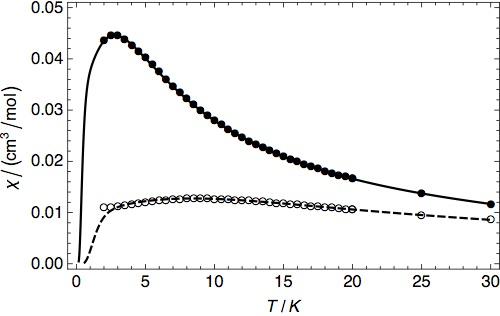
Temperature dependence of the magnetic susceptibility of
Cs2CuCl4 (dots and solid line) and
Cs2CuBr4 (open circles and dashed line). The symbols
represent the experimental data, the lines our theoretical calculation.
- Burkhard Schmidt and Peter Thalmeier: Thermodynamics of anisotropic
triangular magnets with ferro- and antiferromagnetic exchange. New J.
Phys. 17, 073025 (2015)