Many Yb ions

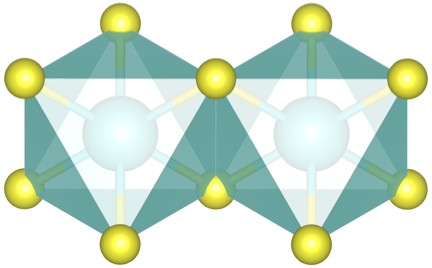
The Yb ions are embedded in distorted octahedra. Coulomb energy on the Yb site is large (several eV), hopping of Yb $f$ electrons via Chalcogen $p$ states to neighboring Yb $f$ states generates superexchange. Instead of trying to determine the symmetry-allowed hopping matrix elements of a tight-binding Hamiltonian and from there «guess» a superexchange Hamiltonian, let’s take things simple: Our exchange Hamiltonian on an effective Yb–Yb bond needs to adhere to its local symmetry as well. The figure above shows one Yb–Yb bond formed by two adjacent distorted YbCh$_\text 6$ octahedra. One distorted octahedron is comprised of two «large» equilateral triangles with edge length $\ell$ and six «small» isosceles triangles with two edges of length $s\ne\ell$ and one edge of length $\ell$. The distorted octahedra are tilted along the Yb–Yb bond such that the large triangular faces are perpendicular to the crystallographic c direction.

By inspection, we find the following symmetries along this bond:

• C$_\text2$ along the bond,
• $\sigma_\text v$ in the middle of the bond,
• i (inversion) in the middle of the bond.

According to Moriya’s rules, the antisymmetric exchange must vanish due to the last criterion. We choose our local cartesian coordinate system such that the $x$ axis points along the Yb–Yb bond, the $y$ axis perpendicular to it in the plane spanned by the $\text{Ch}_4$ rectangle the Yb ion is centered inside, and the $z$ axis parallel to the trigonal axis of a $\text{Ch}_6$ cage. Invariance of the exchange tensor with respect to the symmetry operations above allows for maximally four independent parameters, and we obtain

\[J_{ij} = \underbrace{ \begin{pmatrix} J_\perp&0&0\\ 0&J_\perp&0\\ 0&0&J_\parallel \end{pmatrix} }_{J_\text{av}} + \underbrace{ \begin{pmatrix} J_\Delta&0&0\\ 0&-J_\Delta&J_{yz}\\ 0&J_{yz}&0 \end{pmatrix} }_{J_\text{dd}}\]

for the exchange between the pseudospins on the neighboring Yb sites $i$ and $j$ along the $x$ direction. The first «average» part $J_\text{av}$ is invariant under rotations in the trigonal plane. The traceless directional-dependent part $J_\text{dd}$ is not. It is finite due to the trigonal distortion of the $\text{YbCh}_6$ octahedra. This gives the following expressions:

\[\begin{split} S_i^\alpha J_\text{av}^{\alpha\beta}S_j^\beta &= J_\perp\left(S_i^xS_j^x+S_i^yS_j^y\right) +J_\parallel S_i^zS_j^z \\ S_i^\alpha J_\text{dd}^{\alpha\beta}(\phi)S_j^\beta &= J_\Delta\left[ \cos2\phi\left(S_i^xS_j^x-S_i^yS_j^y\right) -\sin2\phi\left(S_i^xS_j^y+S_i^yS_j^x\right) \right] \nonumber\\ &\phantom{=} +J_{yz}\left[ \cos\phi\left(S_i^yS_j^z+S_i^zS_j^y\right) +\sin\phi\left(S_i^xS_j^z+S_i^zS_j^x\right) \right]. \end{split}\]

Here, $\phi=0,\pm120^\circ$ is the angle of a particular Yb–Yb bond relative to the $x$ direction. Our definition of the exchange constants is made such that it reduces to the standard XXZ model for $J_\text{dd}\equiv0$ which in turn reduces to the standard Heisenberg model for $J_\perp\equiv J_\parallel$.

Expressed with ladder operators, the full effective Hamitonian for the ground-state pseudospin doublet, including an applied magnetic field, eventually is

\[\begin{split} {\cal H} &= \sum_{\left\langle ij\right\rangle}\left\{ \frac12J_\perp\left(S_i^+S_j^-+S_i^-S_j^+\right) +J_\parallel S_i^zS_j^z \right. \\&\phantom{=\sum_{\left\langle ij\right\rangle}} \left. +\frac12J_\Delta\left( {\rm e}^{\text i\phi_{ij}}S_i^-S_j^- +{\rm e}^{-\text i\phi_{ij}}S_i^+S_j^+ \right) \right. \\&\phantom{=\sum_{\left\langle ij\right\rangle}} \left. +\frac1{2\rm i}J_{yz}\left[ {\rm e}^{\text i\phi_{ij}}\left(S_i^zS_j^++S_i^+S_j^z\right) -{\rm e}^{-\text i\phi_{ij}}\left(S_i^zS_j^-+S_i^-S_j^z\right) \right] \right\} \\&\phantom{=} -\mu_0\mu_\text B\sum_i\left[ g_\perp\left(H_xS_i^x+H_yS_i^y\right) +g_\parallel H_zS_i^z \right], \\ \phi_{ij}&= \left\{ \begin{matrix} 0,&\vec R_i-\vec R_j=(\pm1,0,0)\\ \frac{2\pi}3,& \vec R_i-\vec R_j=\pm\left(-\frac12,\frac{\sqrt3}2\right)\\ -\frac{2\pi}3,& \vec R_i-\vec R_j=\pm\left(-\frac12,-\frac{\sqrt3}2\right) \end{matrix} \right.. \end{split}\]

In this representation we can verify that all three terms originating from $J_\text{av}$ all preserve the $z$ component of the total spin $s_z=\sum_is_i^z$ individually while the terms proportional to $J_\Delta$ connect states with $\Delta s_z=\pm2$, and terms proportional to $J_{yz}$ connect states with $\Delta s_z=\pm1$.