The Heisenberg model on a square lattice with competing interactions is one of the most studied models of magnetism in general. In recent years, experimental compounds based on V4+ ions have eventually been realised. We discuss the thermodynamic properties of the model based on exact diagonalization on small clusters and discuss the corresponding experiments.
A quick literature search tells us that there exist more than 1000 papers
on the Heisenberg model on the square lattice with additional
further-than-nearest neighbor interactions, including variants discussing
anisotropies in real space and/or spin space, antisymmetric exchange, ring
exchange, and more. In a large region of parameter space, the exchange
constants are such that it is impossible to find a configuration of
magnetic moments, usually spins, where each individual moment can locally
satisfy a minimum-energy condition on each bond it is connected to
simultaneously. This is termed frustration, which is, according to Siri,
the “disappointment about a futile effort.”
In our context, we may be disappointed about the impossibility to find the
ground state of such a frustrated material easily by extrapolating from
model properties which are local in either real space or reciprocal space.
A central paradigm in physics assumes that by splitting a problem into
understandable pieces one can gain insight into the solution of the full
problem. This is simply wrong for frustrated systems (and many other
material classes), because frustration effects are collective phenomenona
which occur in extended systems only and cannot be understood by simple
extensions of single-particle physics.
The renewed interest in frustrated mangetism in general and in particular
in the frustrated square-lattice model is fueled by the discovery of actual
compounds which can be described by the Heisenberg model with next-nearest
neighbor interactions on the square lattice. The magnetic subsystems of
all these experimentally known compounds are formed by crystal-field-split
Kramers doublets of V4+ ions properly surrounded by oxygens and
embedded into an environment such that well-separated (in terms of exchange
constant magnitudes, not necessarily the crystal structure) layered planes
of these ions are formed. Within a plane, the magnetic ions form a square-
or almost-square-lattice.
Model Hamiltonian and phase diagram
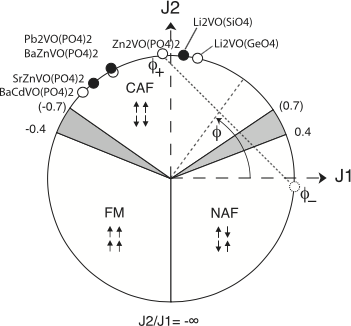
Phase diagram of the frustrated square-lattice Heisenberg model. The FM,
NAF and CAF order (arrows) have wave vectors Q = (0,0), (1,1) and (1,0)
or (0,1) (in units of π/a) respectively. The grey sectors
(J2/J1 values indicated on the outside) represent the
stacked-dimer phase (right sector) and the spin-nematic phase (left
sector). The dotted line corresponds to a constant Curie-Weiss temperature
for the Zn compound with two possible phases, CAF and NAF. Full circles
refer to CAF phases determined by neutron scattering.
Our model Hamiltonian has the general form
$$
{\cal H} = J_1\sum_{\langle ij \rangle_1} {\bf S}_i\cdot{\bf S}_j
+ J_2\sum_{\langle ij \rangle_2} {\bf S}_i\cdot{\bf S}_j
- g\mu_{\text B}\mu_0 {\bf H} \sum_i {\bf S}_i
$$
where $J_1$ and $J_2$ are the nearest- and next-nearest neighbor exchange constants and $B=\mu_0H$ denotes an applied magnetic field. Its phase diagram for $B=0$ consists of three magnetically ordered phases and two disordered phases. All compounds of the ABVO(PO4)2 family have a ferromagnetic nearest-neighbor exchange $J_1$.
Magnetic susceptibility
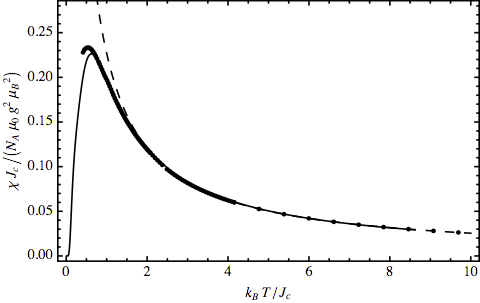
Temperature dependence of BaCdVO(PO4)2. Dots denote
the experimental result, the two curves denote a Curie-Weiss fit to the
high-temperature part (dashed line) and a fit using our finite-temperature
Lanczos data (solid line).
According to Mermin and Wagner, planar magnets cannot order at any finite
temperature, and magnetic ordering is induced by the small but finite
interlayer coupling. However due to the huge number of low-lying (quasi-)
degenerate states frustrated magnetic systems have very low mangetic
ordering temperatures, if at all. Instead the susceptibility shows a
characteristic temperature dependence with a broad maximum followed by a
Curie tail at high temperatures much larger than its characteristic energy
Jc.
Specific heat
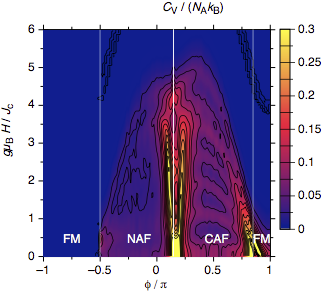
Contour plot of the specific heat of the frustrated square-lattice
Heisenberg model at fixed temperature T = 0.2 Jc, calculated
with the FTL method using a 24-site tile.
We can also determine the temperature dependence of the magnetic part of
the heat capacity. However, as the heat capacity counts all available
states at a given temperature, comparison with experiment suffers from
additional contributions, mainly due to lattice vibrations. Nonetheless
the temperature and value of the maximum heat capacity serves as an
additional tool to determine the exchange parameters of a given compound.
Magnetocaloric effect
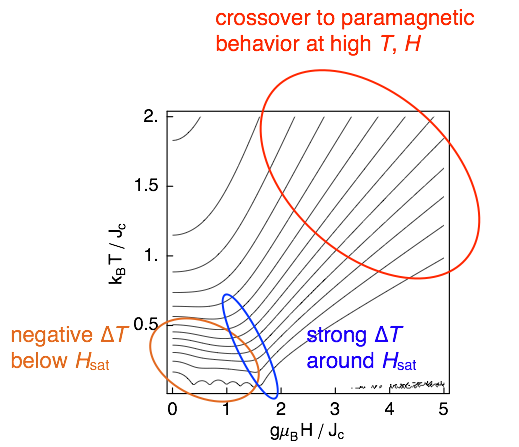
Magnetocaloric effect of the frustrated square-lattice ferromagnet
calculated with the finite-temperature Lanczos method at fixed ratio
J2/J1 with ferromagnetic nearest-neighbor
exchange. The lines are adiabatic curves, the wiggles at low temperatures
are a finite-size effect. For simple paramagnets, the adiabatic curves are
straight lines crossing the origin.
When a crystal containing magnetic ions is placed in a magnetic field the adiabatic or isentropic change of this external parameter causes a temperature change in the sample. This is called the magnetocaloric effect (MCE) which was first described by Pierre Weiss and Auguste Picard 1917 who discovered reversible heating of nickel in the vicinity of its Curie temperature ($354\,^\circ\text C$) when a magnetic field is applied. They found a temperature rise of $0.7\,^\circ\text C$ in a field of $1.5\,\text T$. It is nowadays interesting in several aspects. Firstly suitable compounds, like paramagnetic salts where demagnetization leads to cooling may be used technically. Secondly at high (pulsed) fields the magnetocaloric anomalies at a magnetic phase transition may be used to map out the $B$-$T$ phase diagrams which are not accessible otherwise. Finally it has recently gained special attention in frustrated magnets. There the behavior around the saturation field may be described by the condensation of a macroscopic number of local magnons which leads to a giant enhancement of the magnetocaloric cooling rate. The latter is defined as the adiabatic rate of change of temperature $T$ with magnetic field $B=\mu_0H$. Using a Maxwell relation we can express this with isothermal quantities as
$$
\Gamma_{\text{mc}}:=
\left(\frac{\partial T}{\partial B}\right)_S =
-\frac{\left(\frac{\partial S}{\partial B}\right)_T}
{\left(\frac{\partial S}{\partial T}\right)_B}
= - \frac{T}{C_V}\left( \frac{\partial\bar\mu}{\partial T}\right)_B
$$
where $S$ is the entropy, $C_V$ the heat capacity, and $\bar\mu$ the total magnetic moment of the sample considered (not to be confused with the magnetisation $M=\bar\mu/V$ being the volume density of it). The exchange constants $J_1$ and $J_2$ of all experimentally known compounds are low enough such that the saturation fields for the fully polarized state are actually experimentally accessible. What we can expect from the frustrated square lattice is illustrated at the top of this page.