Strong correlations

Electrons try to avoid each other. If many electrons are confined to the same box, new quantum effects emerge which are summarized under the name correlations. This label reflects the fact that one cannot understand these phenomena in the framework of simple single-particle theories like mean-field or density-functional theories. Although such methods have proven to be very successful, the former maps the presence of “the other” electrons onto an effective potential (the “mean field”), the latter doesn’t care about electronic wave functions but rather maps Schrödinger’s equation onto a problem involving electronic densities only, replacing electron correlations with a more or less arbitrary effective single-particle potential (the “exchange-correlation potential”).

The Hubbard model

A generic model for electron correlations is the one-band Hubbard model with a Hamiltonian

\[H=-t\sum_{\langle ij\rangle,\sigma}c_{i\sigma}^\dagger c_{j\sigma} +U\sum_i n_{i\uparrow}n_{i\downarrow}\]

where the first term describes the kinetic energy of the electrons, gaining energy $-t$ when hopping along a bond between lattice sites $i$ and $j$. The second term describes the Coulomb repulsion $U$ two eletrons have to pay when being on the same place $i$. As long as $U$ is small enough, the kinetic energy gain dominates the total energy of the electrons, and we have a metal. If however $U$ becomes too large, it is energetically favorable for the electrons to avoid each other, hopping only to an adjacent site if this is not already occupied. Thus at a certain value of $U$ at a certain electron density $n$ the Coulomb repulsion dominates, and we have an insulator, which is called a Mott insulator named after Nevill Francis Mott (1905-1996).

Related to this phenomen is the concept of a Wigner crystal: Eugene Paul Wigner (1902-1995) showed that at low enough electron density $n$ the mutual repulsion of the electrons dominates the kinetic energy, basically due to lack of screening. Even free electrons then undergo a metal-insulator transition nowadays called Wigner crystallization.

An early example for a special kind of crystallization on a lattice driven by Coulomb forces of the electrons is the Verwey transition in magnetite Fe₃O₄, first discussed in 1939 by Evert Johannes Willem Verwey (1905-1981), a Dutch chemist. Here the two types of Fe ions Fe²⁺ and Fe³⁺ charge order in a regular fashion such that the Coulomb repulsion of the hopping electrons is minimized.

Two sites

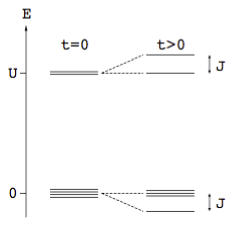
Energy spectrum of the two-site Hubbard model with $J:=4t^2/U$.

To understand the nature of the low-lying excitations emerging from the Hubbard model, it is useful to look at a simple scenario with just two lattice sites. (Regard this as a Hydrogen molecule with orthogonal orbitals and a short-range Coulomb interaction, if you like.) The Hubbard model reads

\[\begin{eqnarray} H &=& -t\sum_{\sigma}\left(c_{1\sigma}^\dagger c_{2\sigma} +c_{2\sigma}^\dagger c_{1\sigma}\right) \\ &&{} +U\left(n_{1\uparrow}n_{1\downarrow} +n_{2\uparrow}n_{2\downarrow}\right). \end{eqnarray}\]

For two electrons (half filling), we have six possible wavefunctions in our basis. Those with singly occupied sites are a singlet and a triplet,

\[\begin{eqnarray*}\left|0,0\right\rangle&=&\frac{1}{\sqrt{2}}\left( \left|\uparrow,\downarrow\right\rangle -\left|\downarrow,\uparrow\right\rangle\right), \\ \left|1,1\right\rangle&=&\left|\uparrow,\uparrow\right\rangle, \\ \left|1,0\right\rangle&=&\frac{1}{\sqrt{2}}\left( \left|\uparrow,\downarrow\right\rangle +\left|\downarrow,\uparrow\right\rangle\right), \\ \left|1,-1\right\rangle&=&\left|\downarrow,\downarrow\right\rangle,\end{eqnarray*}\]

and we have the two wavefunctions with one doubly occupied and one empty site,

\[\begin{eqnarray*}\left|{\rm ex}_{1}\right\rangle&=& \left|\uparrow\downarrow,0\right\rangle, \\ \left|{\rm ex}_{2}\right\rangle&=& \left|0,\uparrow\downarrow\right\rangle.\end{eqnarray*}\]

In this basis, only the singlet couples to the excited states. The corresponding eigenvalues of the Hamiltonian matrix are

\[\begin{eqnarray*}\omega_{1}&=&\frac{1}{2}\left(U-\sqrt{U^2+16t^2}\right) \approx-\frac{4t^2}{U}, \\ \omega_{2}&=&U, \\ \omega_{3}&=&\frac{1}{2}\left(U+\sqrt{U^2+16t^2}\right) \approx U+\frac{4t^2}{U}\end{eqnarray*}\]

plus the three unchanged triplet eigenvalues $\omega_t=0$. The wavefunctions up to second order in $t/U$ are

\[\begin{eqnarray*}e_{1}&\approx&\left(1-\frac{2t^2}{U^2}\right)\left|0,0\right\rangle +\frac{\sqrt{2}t}{U}\left(\left|{\rm ex}_{1}\right\rangle +\left|{\rm ex}_{2}\right\rangle\right), \\ e_{2}&=&\frac{1}{\sqrt{2}}\left(\left|{\rm ex}_{1}\right\rangle -\left|{\rm ex}_{2}\right\rangle\right), \\ e_{3}&\approx&-\frac{2t}{U}\left|0,0\right\rangle +\frac{1}{\sqrt{2}}\left(1-\frac{2t^2}{U^2}\right) \left(\left|{\rm ex}_{1}\right\rangle +\left|{\rm ex}_{2}\right\rangle\right)\end{eqnarray*}\]

plus the three unchanged triplet wavefunctions.

So what has happened? At $t=0$, the singlet and triplet have energy $0$, the excited states have energy $U$, the probability to find a doubly occupied site is exactly $0$. When turning on $t$ (coming from the insulating side), naively one would assume that, at least as long as $t$ is smaller than $U$, nothing changes.

However, despite to the presence of a large Coulomb interaction $U$, as soon as we turn on $t$ the singlet mixes with the doubly occupied states, and we get a small but finite probability to find a doubly occupied site in the ground state. Even more: The ground state is energetically lowered by $J:=4t^2/U$, see the schematic spectrum above. From a single-particle point of view, this would be completely impossible. Later on we will see that the energy gain $J$ relates to spin fluctuations and is of fundamental importance for the emergence of magnetism.

This is a purely quantum mechanical many-body effect which classically doesn’t exist. It is based essentially on three requirements: The Heisenberg uncertainty principle (if we are fast enough, we can violate energy conservation for a short time to create a double occupancy), the Pauli principle (no two Fermions can occupy the same state), and the indistinguishability of the electrons (after an electron hop creating a doubly occupied site, we don’t know which electron then hops away to remove the double occupancy). This phenomenon is the very origin of many kinds of magnetism, be it the undoped parent compounds of the cuprate high-temperature superconductors, or many other insulating magnets like the frustrated systems we are interested in.